![]() - - -Evans Engineering Logo- - -
- - -Evans Engineering Logo- - -![]()
The Evans Engineering Logo is an image of three straight lines in Poincare Geometry
Poincare Geometry is based on a semi-infinite plane representation of all lines. A Poincare Line consists of two points within the semi-infinite plane connected by an Euclidean (plane) Geometry semi-circle with the center on the edge of the semi-infinite plane. The ends of all the semi-circles will be perpendicular to the edge of the semi-infinite plane. For the Evans Engineering Logo, the edge of the semi-infinite plane is to the right, where all the Poincare Lines (Euclidean Semi-Circles) terminate.
The representation in the Evans Engineering Logo is 3 Poincare Lines. One line does not intersect the other two. Two of the lines intersect at a point centered to the left. The 3 Poincare Lines represent a line with two external lines intersecting at a single point. This is similar to a figure which might be drawn to illustrate the Euclidean Parallel Line Postulate, with notable exceptions!
In the Euclidean Parallel Line Postulate, through a point external to a line, one and only one line can be drawn which does not intersect the original line. Euclid stated this as a postulate, concluding that it could not be proved as a theorem from any of his other postulates. The Poincare representation is one of many now known geometries in which Euclid's Parallel Postulate does not hold - others being spherical and elliptical geometries in which parallel (non-intersecting) lines cannot be drawn and various hyperbolic geometries in which multiple non-intersecting (parallel) lines can be drawn.
In this Poincare representation, all the Poincare Lines that can be drawn between the two intersecting lines also do not intersect the third line. In Poincare Geometry, there are an infinite number of lines which can be drawn which go through the same point of intersection but also do not intersect the third line.
Parallel lines are straight (shortest distance between two points) and non-intersecting. They are not necessarily equal distant. In the classic representation of parallel lines as being equidistant straight lines "like railroad tracks" it should be noted that at most one rail can actually be straight (a great circle) on the surface of the earth. The other rail will not be straight (i.e. not the shortest distance between two points on the rail). The railroad tracks are equidistant curves, but are not parallel because they are not straight.
A detailed description of Poincare Geometry can be found in: Herbert Meschkowski (1964) Noneuclidean Geometry, Academic Press, New York.
The Poincaré half-plane model is illustrated in Wikipedia.
The distance metric in the Poincare half-plane model is:
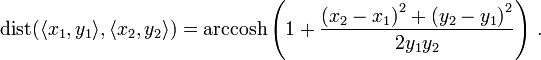
A Poincare Circle was constructed from the method in the Wikipedia article. The Poincare center is at C. Diameters through the poincare center were constructed every 45 degrees. The distance from C to the circle along any radii was constant when measured by the Poincare distance metric. Circles transform to circles in Euclidian space. The Euclidian center is at E. The radii or diameters are shortest distance straight lines in both geometries, but the location of the centers is not congruent. I measured the distance from A to B along the diameter, using the distance metric, and along an Euclidian straight line using ten small Poincare straight line approximations. The Euclidian straight line is just over six percent longer than the Poincare Diameter, in Poincare space.
The Poincare Circle is illustrated following: